| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 과학적 시각화
- illustrator
- pgAdmin
- 알 수 없는 좌표계
- Matrix
- shp파일 좌표계
- 공간적 자기상관성
- 정방 행렬
- Python
- 행렬의 뺄셈
- 프로젝트 좌표계
- 이미지 깨짐 해결
- 행렬
- QGIS
- 블렌더
- 파이썬
- 일러스트레이터
- 행렬 표기
- django
- 일러스트
- 벡터와 행렬의 관계
- Blender
- PyCharm
- PostgreSQL
- scientific visualization
- spatial autocorrelation
- 분산
- 이미지 연결
- 이미지 파일 저장
- 평균
- Today
- Total
주석으로 채워가는 대학원생의 연구 노트
공간적 자기상관(Spatial Autocorrelation)이란 - 공간적 인접성, 공간가중행렬, Moran’s I 지수, Geary’s G지수 본문
공간적 자기상관(Spatial Autocorrelation)이란 - 공간적 인접성, 공간가중행렬, Moran’s I 지수, Geary’s G지수
밤샘노트 2025. 2. 8. 00:49

# 공간적 자기상관(Spatial Autocorrelation)이란
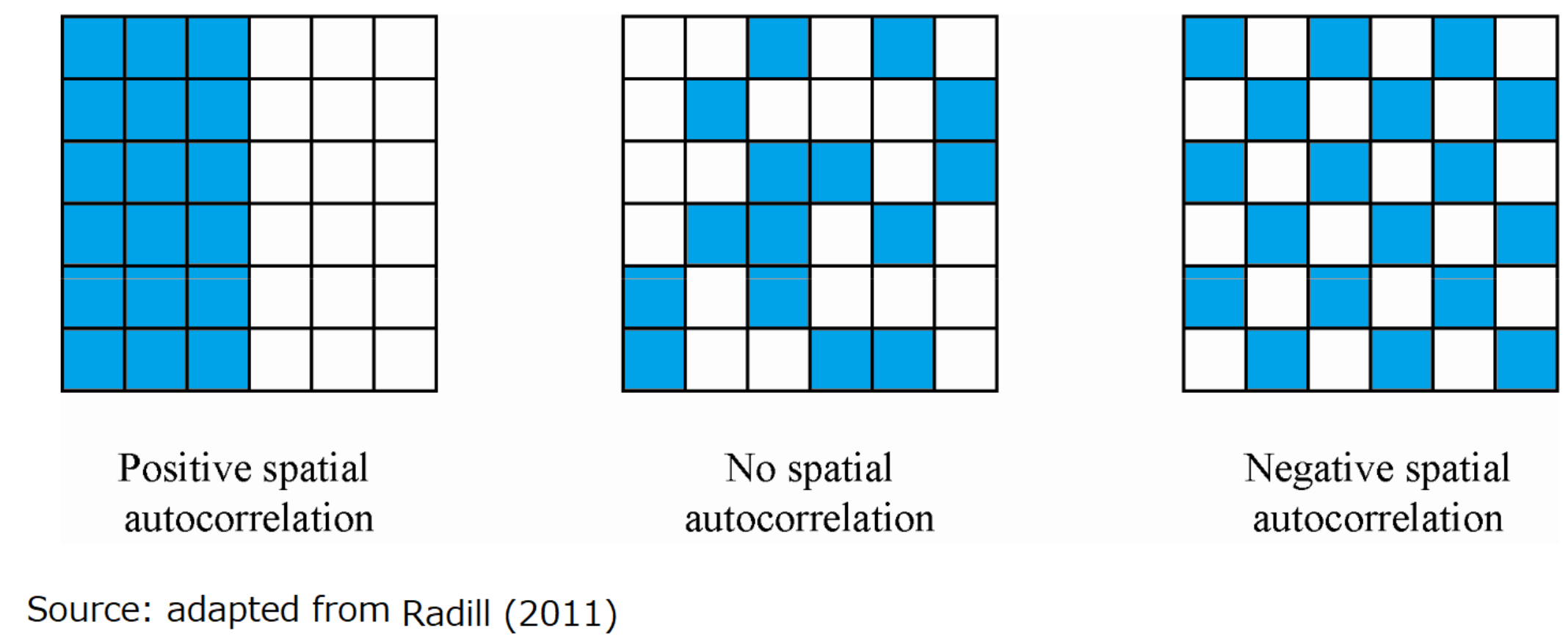
공간적 자기상관이란 한 지역에서 나타나는 특성이 인접한 지역에서도 비슷한 경향을 보이는지를 설명하는 개념이다.
즉, 공간적으로 가까운 지역일수록 비슷한 특성을 보이고, 멀리 떨어진 지역일수록 차이를 보이는 경향이 이다.
예를 들어
- "가까운 지역끼리 비슷한 특성을 가지는가?"
- "멀리 떨어진 지역끼리는 다른 특성을 가지는가?" 를 분석하는 개념이다
공간적 자기상관이 높을수록 인접한 지역 간의 특성이 유사하고, 낮을수록 특성이 무작위적으로 분포한다.
따라서 공간적 자기상관을 측정하는 것은 공간 분석에서 중요한 과정이다.

# 공간적 자기상관을 측정하기 위한 기준
공간적 자기상관을 수치화하기 위해 다양한 방법이 사용되며,
이를 위해 먼저 공간적 인접성(spatial neighborhood)을 정의해야 한다.
공간적 인접성은 특정 지역(지점 또는 면)이 얼마나 가깝고, 어떤 방식으로 다른 지역과 연결되는지를 결정하는 기준이다.
일반적으로 다음과 같은 방식으로 정의된다.
- 거리 기반 인접성(Threshold Distance)
- 특정 지점에서 일정 거리(임계 거리) 내에 위치한 지역을 이웃으로 간주하는 방법
- 물리적 접합(Spatial Contiguity)
- 면(polygon) 데이터에서 물리적으로 접하고 있는 지역을 이웃으로 정의하는 방법
공간적 인접성이 정의되면, 이를 바탕으로 공간적 자기상관을 측정할 수 있으며,
공간적 관계를 설정하는 방식에 따라 고려될 수 있는 접합 유형이 크게 세 가지 존재한다.
# 공간적 접합유형(Spatial Contiguity Types)
공간적 자기상관을 측정할 때, "어떤 지역을 이웃으로 간주할 것인가?"를 결정하는 기준이 필요하다.
이에 따라 대표적으로 다음과 같은 세 가지 유형이 있다.
- Rook(루크) 방식
- 상하좌우(4방향)로 직접 접한 지역만 이웃으로 간주하는 방식
- 체스에서 '루크(Rook, 룩)'가 상하좌우로 움직이는 방식에서 유래함
- 예시: 정사각형 그리드에서 네 변이 맞닿아 있는 지역만 이웃으로 정의됨
- Bishop(비숍) 방식
- 대각선 방향으로만 연결된 지역을 이웃으로 간주하는 방식
- 체스에서 '비숍(Bishop, 비숍)'이 대각선으로만 이동하는 방식에서 유래함
- 예시: 정사각형 그리드에서 꼭짓점끼리 맞닿아 있는 지역만 이웃으로 정의됨
- Queen(퀸) 방식
- 상하좌우 + 대각선(8방향)을 모두 고려하는 방식
- 체스에서 '퀸(Queen, 퀸)'이 모든 방향으로 이동할 수 있는 특징에서 유래함
- Rook 방식과 Bishop 방식을 결합한 형태로, 가장 넓은 범위를 이웃으로 간주함

# 공간적 자기상관을 측정하는 방법 : 인접행렬과 공간가중행렬
1. 인접행렬
- 인접행렬은 각 지역이 서로 이웃인지 아닌지를 나타내는 행렬이다.
- 예시
- 예를 들어, 9개의 지역이 있을 때, 두 지역이 이웃하면 행렬의 값은 1, 이웃하지 않으면 0이 된다.
- 이를 통해 지역 간의 단순한 공간적 관계를 파악할 수 있다.

2. 공간가중행렬
- 공간가중행렬은 인접행렬을 기반으로 지역 간 관계를 보다 구체적으로 표현한 행렬이다.
- 다시 말해, 공간가중행렬은 분석 대상 지역 내 여러 지점(또는 하위 지역) 간의 공간적 인접 여부를 정리한 행렬이다.
- 이 행렬을 활용하면 지역 간의 특성(소득, 인구 밀도 등)이 주변 지역과 어떤 상관관계를 가지는지 분석할 수 있다.
- 구축 방법
- 공간가중행렬은 지역 간의 인접성을 정의하는 기준에 따라 구축된다.
- 인접성
- 지역 간 인접성은 공간적 관계를 정의하는 방법에 따라 달라진다.
- 앞서 설명한 '접합 유형(Rook, Bishop, Queen)'을 적용하여 공간가중행렬을 생성할 수 있다.

# 공간가중행렬의 크기
공간가중행렬의 크기는 N × N이며, 여기서 N은 분석 대상이 되는 지역의 개수를 의미한다.
- 예를 들어, 분석 대상 지역이 10개라면 행렬의 크기는 10 ×10이다.


⁉️ 행렬이 뭐예요 ⁉️
글쓴이와 같이 행렬에 대해 잘 모르는 독자들을 위해 이 포스팅에서 다루는 행렬에 대해 개념만 짚고 넘어가자.
# 행렬(Matrix)이란
행렬은 숫자나 값을 직사각형 모양으로 정리한 표를 말한다.
# 행렬의 구성요소
- 행(Row) : 행렬의 가로줄
- 열(Column) : 행렬의 세로줄
예를 들어, A와 B라는 두 지역 간의 관계를 나타내는 행렬은 다음과 같다.

- 첫 번째 행은 A와 다른 지역 간의 관계(A와 B)를 나타낸다.
- 두 번째 행은 B와 다른 지역 간의 관계(B와 A)를 나타낸다.
# N × N 행렬의 구조
N × N 행렬에서 N은 분석에 포함된 지역의 개수이며, 행렬은 가로로 N개, 세로로 N개의 값을 가진다.
행렬의 각 값은 특정 지역과 다른 지역 간의 관계를 나타낸다.
A, B, C 지역의 관계를 표현하는 행렬은 다음과 같다.
- 행렬(Row) : A, B, C 지역을 가로 방향으로 나열
- 열(Column) : A, B, C 지역을 세로 방향으로 나열

- 행렬의 값
- 1 : 두 지역이 서로 이웃한 경우
- 0 : 두 지역이 이웃하지 않은 경우
- 0 : 자기 자신과의 관계(A와 A, B와 B 등)는 표시하지 않음
# 행렬의 크기
행렬의 크기는 분석 대상 지역의 개수(N)에 따라 결정된다.
예시
- 10개의 지역이 있다면 행렬은 10×10 크기를 가진다.
- 100개의 지역이 있다면 행렬은 100×100 크기를 가진다.
- 1,000개의 지역이 있다면 행렬은 1,000×1,000 크기를 가진다.
지역의 수가 많아질수록 행렬의 크기가 커지며, 계산이 복잡해질 수 있다.
하지만 이는 지역 간의 관계를 보다 정밀하게 분석할 수 있게 해준다.
# 요약
- N : 분석 대상 지역의 개수
- N × N 행렬 : 각 지역 간의 관계를 체계적으로 정리한 표
- 행렬의 크기 : 두 지역 간의 관계(인접 여부)를 나타냄
이제 행렬의 기본 개념을 이해했으니, 다음 주제를 살펴보도록 하자.
# 데이터 유형에 따른 공간적 자기상관 측정 방법
공간적 자기상관 분석은 데이터 유형에 따라 분석 방법이 달라진다.
1. 명목자료
- 정의
- 명목자료는 분류를 위한 데이터로, 숫자에 특별한 크기나 순서가 없다.
- 예시: 땅의 용도(주거, 상업, 농업), 투표 결과(찬성/반대)
- 접합 조합(BB, BW, WW)
- 명목 자료의 경우, 이웃한 두 지역 간 데이터가 같은지, 다른지에 따라 다음과 같이 구분된다.
- BB(Both Black) : 두 지역 모두 같은 값을 가질 때 (예시: 둘 다 주거지)
- BW(Black-White) : 두 지역이 서로 다른 값을 가질 때 (예시: 하나는 주거지, 하나는 상업지)
- WW(Both White) : 두 지역 모두 같은 값을 가질 때 (예시: 둘 다 상업지)
- 분석 방법
- BB, BW, WW의 빈도를 계산하여 패턴을 분석한다.
- 예를 들어, 주거지가 특정 지역에 몰려 있는지, 무작위로 섞여 있는지 알 수 있다.
- 명목 자료의 경우, 이웃한 두 지역 간 데이터가 같은지, 다른지에 따라 다음과 같이 구분된다.
2. 등간자료와 비율자료
- 등간자료
- 숫자 간의 차이를 비교할 수 있지만, 절대적 기준(0점)이 없는 데이터
- 예시: 온도(섭씨), 시험 점수
- 비율자료
- 숫자 간의 차이를 비교할 수 있고, 0점이 기준이 되는 데이터
- 예시: 키, 몸무게, 소득
- Moran’s I와 Geary’s G 이 두 지수는 등간자료와 비율자료에서 공간적 자기상관을 측정하는 대표적인 방법이다.
# Moran’s I 지수
Moran's I 통계량은 공간 데이터를 분석할 때, 특정 지역의 값들이 주변 지역의 값들과 얼마나 비슷하거나 다른지를 수치로 나타내는 지표이다.
이 지표는 연구 대상 지역에서 비슷한 값들이 한곳에 모여 있는지(군집 경향), 아니면 서로 다른 값들이 섞여 있는지를 확인하는 데 사용된다.
모란지수는 두 가지 정보를 활용하여 계산된다.
- 공간가중행렬 : 지역 간의 인접 관계를 나타내는 표
- 속성 데이터의 유사성 : 이웃한 지역들 간의 값이 얼마나 비슷한지를 측정한 값
쉽게 말해, "비슷한 값들이 가까운 지역에 모여 있는가?" 혹은 "서로 다른 값들이 섞여 있는가?"를 하나의 숫자로 표현한 것이다.

- Moran's I 지수의 값
- 모란 I 지수는 -1부터 1사이의 값을 가진다.
- I = 1 (완전한 양(+)의 자기상관)
- 비슷한 값(예: 높은 값들)이 서로 가까운 지역에 모여 있는 경우
- 예시: 집값이 높은 지역끼리 몰려 있거나, 집값이 낮은 지역끼리 몰려 있는 경우
- I = 0 (자기상관 없음)
- 값이 무작위로 분포되어 있어 이웃 지역 간의 특별한 패턴이 없는 경우
- I = -1 (완전한 음(-)의 자기상관)
- 높은 값과 낮은 값이 규칙적으로 섞여 있는 경우
- 예시: 부유한 동네와 가난한 동네가 번갈아 나타나는 패턴
- I = 1 (완전한 양(+)의 자기상관)
- 모란 I 지수는 -1부터 1사이의 값을 가진다.

- Moran's I 지수의 한계
- 모란 I는 값이 비슷한 지역들이 모여 있다는 걸 알려주지만, 값이 높은 군집인지, 낮은 군집인지 구분하지 못한다.
- 예를 들어,
- 집값이 높은 지역이 모여 있거나, 낮은 지역이 모여 있는 경우 → 둘 다 모란 I 값이 높게 나온다.
- 따라서 어떤 값이 군집을 이루고 있는지 알기 위해서는 추가적인 분석이 필요하다.
# Geary’s G 지수
Geary's G 통계량은 공간적 자기상관을 측정하는 방법 중 하나로,
특정 값들의 군집 형태(특히 큰 값과 작은 값의 군집)를 구별하는 데 유용한 지표이다.
쉽게 말해, 큰 값(예: 높은 소득, 높은 집값)과 작은 값(예: 낮은 소득, 낮은 집값)이 각각 모여 있는지를 살펴볼 수 있다.

- Geary's G 지수의 값
- G 통계량은 0에서 1 사이의 값을 가진다.
- G(d) 값이 1에 가까운 경우
- 큰 값들(예: 높은 소득, 높은 집값)이 특정 지역에 및집되어 있음을 나타낸다.
- 예시: 부유한 지역끼리 모여 있는 경우
- G(d) 값이 0에 가까운 경우
- 큰 값들이 특정 지역에 몰리지 않고, 무작위로 분포되어 있음을 나타낸다.
- 예시: 높은 소득이나 높은 집값이 특정 지역에 치우치지 않고 고르게 퍼져 있는 경우
- G(d) 값이 1에 가까운 경우
- G 통계량은 0에서 1 사이의 값을 가진다.
- Geary's G 지수의 특징
- Geary's G 지수는 값의 차이를 중심으로 분석한다.
- 큰 값의 군집과 작은 값의 군집을 구별할 수 있다.
- 큰 값들의 군집 패턴을 중심으로 분석하므로, 작은 값들의 군집에는 낮은 값을 산출한다.
- Geary's G 지수는 Moran's I 지수의 한계를 보완하는 역할을 한다.
# Moran's I 지수와 Geary's G 지수 비교
Moran's I 지수와 Geary's G 지수는 모두 공간적 자기상관을 측정하지만, 다음과 같은 차이가 있다.
| 특징 | Moran's I | Geary's G |
| 측정 방식 | 값의 유사성을 측정 | 값의 차이를 측정 |
| 군집 구별 | 큰 값과 작은 값의 군집 구별 X | 큰 값과 작은 값의 군집 구별 O |
| 값의 범위 | -1 ≤ I ≤ 1 | 0 ≤ G ≤ 1 |
| 보완적 활용 | 큰 값과 작은 값의 구별 없이 전체 패턴 분석 | 값의 차이에 초점을 맞춰 분석 |
# 다음 포스팅 예고
" 공간적 자기상관성의 유의성 검정 "
# 참고자료
이번 포스팅에서는 아래 사이트를 참고하여 정리하였습니다.
저작권이나 기타 문제가 있을 경우 알려주시면, 즉시 검토하고 수정하겠습니다.
https://product.kyobobook.co.kr/detail/S000000453694
고급통계분석론 | 이희연 - 교보문고
고급통계분석론 | 고급통계분석의 이론과 실습을 병행하여 소개하는 『고급통계분석론』. 이 책은 통계이론과 원리에 대한 기초를 확립한 후 통계분석 방법을 배우도록 유도한다. 연구 목적에
product.kyobobook.co.kr
공간적 자기상관성과 관내사전투표와 본투표의 투표율: 제21대 총선 서울시 동별 분석
이 연구는 공간적 자기상관성(spatial autocorrelation)이라는 개념을 사용해 한국 선거를 처음으로 분석했다는 점에서 의미가 있다. 공간적 자기상관성이란, 공간상의 한 위치에서 발생하는 사건은
www.kci.go.kr
https://foss4g.tistory.com/1855
ESDA: 공간 자기상관(Spatial Autocorrelation) 분석 소개
안녕하세요? 이번 글은 파이썬의 ESDA 패키지를 통한 '공간 자기상관(Spatial Autocorrelation)' 실습 과정을 정리해 보겠습니다. 이 글은 캐나다 Clearly에서 데이터 및 분석 리더로 활동하시는 Peng Wang(펭
foss4g.tistory.com
https://suyeon96.tistory.com/32
[자료구조] 그래프 (Graph) - 인접행렬 vs 인접리스트, DFS, BFS, Connected Component, Spanning Tree
1. 그래프 1.1 그래프란? 그래프(Graph)란 요소들이 서로 복잡하게 연결되어 있는 관계를 표현하는 자료구조이다. 그래프는 정점(vertex)과 간선(edge)들의 집합으로 구성된다. G = (V, E) 수학적으로 그
suyeon96.tistory.com
https://homicide-disparities-colombia.netlify.app/
Regional Disparities, Aggregation Effects and the Role of Space
homicide-disparities-colombia.netlify.app
'Spatial Analysis > 통계' 카테고리의 다른 글
| 행렬(Matrix) 계산하는 방법 - 행렬의 덧셈과 뺄셈, 곱셈, 전치 행렬 (0) | 2025.03.15 |
|---|---|
| 행렬(Matrix) 기본 개념과 표기법 - 행렬, 행과 열, 정방 행렬, 행렬 표기, 벡터, 벡터장의 개념, 벡터와 행렬의 관계 (1) | 2025.03.14 |
| 공간적 자기상관성(Spatial Autocorrelation)의 표본 추출 방식 - 자유 표본 추출, 비자유 표본 추출, 기대값(평균), 표준편차의 개념 (0) | 2025.02.24 |
| 점 추정(Point estimation)의 개념 - 추론 통계, 모수, 점 추정, 추정량, 추정치의 개념 (1) | 2025.01.28 |
| 포아송 분포(Poisson distribution)란 - 이산 확률 분포, 포아송 분포 (3) | 2025.01.21 |




